フリーランス 2 年目の振り返り

はじめに

今年はフリーランスとしては 2 年目になる年でした。

2 年目もなんとかフリーランスのエンジニアとしてやっていくことができたので、去年と同様にこの 1 年を振り返ってみようと思います。

実績

今年は 5 社と契約し、5 つのプロジェクトに携わりました。

5 社のうち 2 社は去年から引き続き契約していただいたクライアントで、残りの 3 社は今年新規に契約することになったクライアントでした。

またその新規の 3 社のうちの 2 社は旧知の方からの紹介やオファーでした。

仕事内容としてはデータエンジニアが主で、その他には開発コンサルのようなこともしました。

仕事で新しく使ったツールやサービスは以下のようなものがありました。

• dbt
• Dataform
• Terraform
• trocco
• AirFlow
• Looker
• Looker Studio (旧 Google データポータル)
• Amazon QuickSight
• Firebase
• AWS Amplify
• Rust

売上は去年と比べると約 1.7 倍に増えました。

また通算で 1 社あたりの平均契約月数は 10.6 カ月に増えました (去年は 7.3 カ月)。

数字としては去年よりも良い方向に変化しており、仕事内容もやりたい方向の業務に携わることができたので満足のいく 2 年目になりました。

具体的な業務内容

今年の主な仕事だったデータエンジニアと開発コンサルについて、具体的な内容を振り返ってみます。

データエンジニア

データエンジニアとしてはそれぞれ特徴の異なるいくつかの現場を経験しました。

データ活用が盛んな組織での業務

まずは既にデータ活用が盛んな組織でデータエンジニア／データアーキテクトチームの一員として参加した現場でした。

そこでは既に BigQuery を中心とした大規模なデータ基盤があり、データエンジニア／データアーキテクトや分析担当者がそれぞれ専任で多数在籍しており複数チームを組んでいるような組織でした。

その現場では私は主に他社がリリースした新サービスや新機能を導入するための調査やプロトタイプの実装を担当しました。

例えば Dataform や dbt の導入プロジェクトのための調査を行い、既存のクエリを移植するためのサンプルを実装してドキュメントを整備しました。また trocco を AirFlow のデータパイプラインに組み込むために API を調査し、AirFlow から trocco を使えるようにするカスタムオペレーターを実装したりもしました。

またチームはデータエンジニアのチームでしたが、メンバーの中には IT システムに強くない方もいらっしゃるので、システム的なトラブルや複雑なエラーが出たときに私が引き継いで問題を解消するといった役割を担うことも少なくありませんでした。

チーム全体としてはデータマネジメントを意識してタスクを組んでいる印象で、この規模でデータ活用をしている組織ではデータマネジメントは今後ますます重要視されてくると感じました。

データ活用文化のない組織での業務

こちらは大きな組織でエンジニアも多数在籍しており自社サービスを展開しているものの、データを活かしたサービス開発はしていない現場でした。

私は始めはデータエンジニアとしてではなく小回りの利くなんでも屋のような役割で参加したのですが、業務の流れでサービスのユーザーの行動を可視化する例を示すことになりました。

その現場ではサービスを展開しているもののユーザーがどれくらいの頻度で使っているかが分からないという課題がありました。元々そういった分析をする方針であればアプリケーションに Google Analytics 等を組み込んでおくこともできますが、この場合はそういった仕組みは使っておらず、使えるのは基盤として使っている AWS のログだけでした。幸いにそのアプリケーションはユーザー認証に Cognito を使っており、Cognito は認証イベントを CloudTrail にログ出力するようになっていたのでそのログを Athena でクエリできるように整備し QuickSight でユーザーのログイン頻度やアクティブユーザー数等を可視化することができました。

まだ始めの一歩ですが、こういったステップを続けてサービス作りにデータを活用する効果が社内に認められて、より活発にデータを活用する文化にできたらよいなと思った現場でした。

データ活用文化のないスタートアップでの業務

こちらでは自社サービスを展開しているスタートアップで、サービスの利用状況を把握するために役割を超えて幅広く手を動かした現場でした。

私がチームに参加したちょうどその頃、サービスの状況を把握するためにウォッチするべき KPI を定める議論をしていたところでした。

私もそのミーティングに参加し、幾度かの議論を経て定まったサービスの KPI を追えるダッシュボードを作り始めました。

しかしその時点ではユーザーの行動を追える情報はサーバー側に存在しなかったので、まずは Google Analytics のコードをフロントエンドのコードに追加し、興味のあるイベントが起こったときにそれを補足できるようにしました。

またバックエンドはマイクロサービスの作りになっており DB も個々に持っていたので、それらのデータを一つの BigQuery に集約するデータパイプラインも構築しました。

他にもメール送信機能は外部サービスを使っていたりしたので、メールに関するログを外部サービスから取得して BigQuery に投入する仕組みも構築しました。

そうして各所からのデータが集まるデータレイクが出来上がったので、それをデータ変換する仕組みを dbt で作り、ダッシュボードで可視化するためのパイプラインを整えました。

ダッシュボードは Google データポータル (現 Looker Studio) を使って実現し、定めた KPI 以外にもそれに繋がる重要な指標を把握するチャートも用意して、サービス開発の定例で参照するという流れを確立しました。

この現場では少人数のチームであり自分でプログラムに手を入れたりインフラを変更したりできる環境だったため、サービス作りにデータを活用する新たな流れを導入できたよい経験になりました。

開発コンサル

こちらは業務内容としては上とは変わって、サービス開発を技術的な点からサポートする役割をする現場でした。

相手方は医療ドメインの専門家の方で、そのドメインをターゲットにした Web サービスを開発してリリースするために必要なサポートを提供するという仕事内容でした。

始めはサービスのコアとなるある問題を解くためのプログラムがローカルにあるだけの状態で、その機能を Web で提供するのがひとまずの目標でした。

私の役割としては Web アプリケーションとして仕上げるためのシステムアーキテクチャの提案、技術選定のアドバイス、ユーザーエクスペリエンスを意識したサービス利用フローの提案、それを開発するための開発プロジェクトの進め方の提案などでした。

ここでは自分のコンピューターサイエンスのバックグラウンドや、新規サービスの構想から実装してリリースまでやり遂げた経験からできるサポートを提供する形でした。

この案件は相手方はターゲットとなる事業ドメインの専門家であり当時から既に具体的なユーザーが見えていたものの、後はシステム化のノウハウだけが足りないという現場だったので、自分の提供できるものと非常にマッチした仕事でした。

評価

2 年目である今年は仕事内容としては自分の目指していきたい方向と合致したものばかりで楽しく仕事ができたのでよかったです。

顧客からの評価もおおむね良く、長く契約していただけるケースが増えました。

頂いたフィードバックとしては

• 「あいまいな指示でもうまく要件を咀嚼してこなしてくれて助かる」
• 「技術的なスキルが優れているので難しいタスクを任せやすい」
• 「ドキュメントを丁寧にまとめてくれる」

などがありました。

また過去の私の仕事を評価していただいた方から頂いた案件が今年は二つあり、これもよい出来事でした。

今後もこの調子で今の顧客を大切にしつつ、評価され続けるような仕事ぶりを維持していきたいと思います。

これから

今後も基本はデータエンジニアとして仕事を受けつつ、開発コンサルも求められればやっていく方針でいこうと思います。

去年から継続してデータ活用の現場に触れてきた感触として、データ活用に積極的な組織ではデータマネジメントに注力していきつつあることが分かったので、そういった方面の知識や経験も積んでいこうと思います。

特にデータの品質担保のためのテストの仕組み、幅広いメンバーのデータ理解のためのメタデータ管理、各種法規の遵守のためのセキュリティなどが直近の課題として捉えられている印象だったので、そういった方面でも仕事ができるように準備していきたいと思います。

それでは 3 年目もどうぞよろしくお願いします。

フリーランスになって 1 年経ったので振り返り

はじめに

私は 2021 年の初めに前職を退職してフリーランスのエンジニアになりました。

そろそろフリーランスになってちょうど 1 年経つので、この 1 年間の活動をまとめつつ、その中で感じたよかったこと・よくなかったことを振り返ってみようと思います。

この 1 年の活動

フリーランスとしては 3 社と契約し、案件としては 4 つの案件を頂きました。

仕事の種類としては Web システムの開発やデータ基盤の構築・運用が主でした。

案件をこなす中で技術的に新しく身についたことを挙げると次のようなものがあります。

• Golang
• TypeScript
• React
• Three.js
• GCP (特に BigQuery 等のデータ処理系のサービス)

総合的に見ると、フリーランスになったことは自分の人生にとってよい方向の決断だったと感じています。

以下、具体的に掘り下げていきます。

フリーランスになって良かったこと

人間関係でのストレスがなくなった

これが一番よかったと感じることです。

企業勤めをして組織の一員として働いている間は、人間関係に端を発するいろんなストレスがありました。それらは当時から自覚していたものもあれば、時間が経った今だからこそ自覚できたものもあります。

そういった人間関係に関するストレスが、フリーランスとして 1 年活動してきた中ではほとんど (あるいは全く) 発生しませんでした。

いくつか思い当たる理由はありますが、一つ言えるのはフリーランスになったことで個々の組織に対する依存が薄まって組織との関係が「疎結合」になり、人間関係に悩むほどの過度な期待を他者に求めなくなったのが大きいのではないかと思います。

こと労働においては「かけがえのない、替えの利かない一つの組織」に執着するよりも、いくつかの組織と関係を持ちながらそれぞれを相対化して見ることのできるフリーランスとしての働き方のほうが、自分には合っているようです。

自分でコントロールできることが増えた

人が集まって組織として行動すると、やはりアンコントローラブルなことが多くなりそれがストレスになることもあります。

フリーランスになってからは、例えば自分の意志で仕事の種類を選択したり、稼働日数を調節して業務時間をコントロールしたり、また仕事のために使うお金は自分で使い道を選択したりできるようになり、そしてそれらのことを決定するのに誰かに稟議を通したりする必要もなくなりました。

人事評価もなくなり、自分の仕事への評価はクライアントとの契約の継続更新と事前に合意した報酬額となり、シンプルになりました。

個人ではできない大きなことをするために会社を作り人が集まるわけですが、フリーランスとして個人で意思決定し小回りの利く働き方のほうが、今の自分には合っていると感じました。

収入が増えた

これは明確に数値として結果に出るので、モチベーションに繋がりました。

1 年目となる今年は会社勤めをしていた頃の 3 倍の額を稼ぐことができ、フリーランスとしてやっていく自信にもなりました。

仕事に使ったスキルは会社勤め時代とほぼ変わらないのですが、環境を変えるだけで収入は大幅に変わりました。環境によって働き方や収入が大きく違うのは当然として、フリーランスはそういったよりよい環境を常に探し選択していきやすい働き方なのだと思いました。

フリーランスになって悪かったこと

先行きが不透明になった

フリーランスはそういうものだという話なのですが、やはりこの 1 年の仕事と収入を来年も維持できるかというとその保証はないですし、10 年後もフリーランスとしてやっていけるかは分かりません。

しかしそれでも打てる対策はあって、それは例えば請ける仕事を複数にして収入を失うリスクの分散をしたり、流行りの技術をむやみに追いかけずに基礎となる理論をしっかり身に着けて個々の現場での対応力を磨いたりといったことをしています。

チームで大きなことができなくなった

フリーランスとしては客先には準委任契約の業務委託として参加しており、基本的には顧客がやりたいことをお手伝いする形になります。

顧客ごとに持っているいろいろな「やりたいこと」に触れてその実現に参加できるのはそれはそれで楽しいのですが、一方で自分が「やりたいこと」を見つけた時にそれを実現するに当たって「会社」の持つリソースを活用することはできなくなったのだと実感しました。

「早く行きたければ一人で進め、遠くまで行きたければ皆で進め (If you want to go fast, go alone. If you want to go far, go together.)」という言葉がありますが、まさにこのことを言い表していると思います。

これからのこと

フリーランスとして 1 年活動してきて、幸いにも客先からも評価して貰えており、これからもしばらくはやっていけそうだという自信がつきました。

目標としては 30 代の間、あと 9 年は続けられるようにいろいろと試行錯誤していきたいと思います。

方針としては一つのスキルを突き詰めて高い単価を目指すのではなく、広くいろんな現場に対応できるようにスキルを広げていき、仕事に多様性を持ちつつリスクを分散して、また収入のスケールアウトを目指していこうと思います。

それでは 2 年目もフリーランスとして、どうぞよろしくお願いします。

30 年前の Python 0.9.1 をコンパイルして動かしてみた

この記事は はんなりPython Advent Calendar 2020 の 16 日目の記事です。

関西でフリーランスのエンジニアをやっている @tsujio です。データ分析とか分析基盤のお仕事を承っています。

今日のインターネットには Python の最新情報がたくさん流れていますが、この記事では Python の歴史にフォーカスを当ててみます (最新情報だとネタがないので)。

2020 年 12 月時点での最新バージョンは 3.9 で、最近は型に関する機能がどんどん追加されていってます。しかし今回は今からおよそ 30 年前の、Python が世に初めて出た 1991 年時点のソースコードをダウンロードして動かしてみようと思います。

Python 初出

Wikipedia の History of Python を読むと、Python が初めて世に出たのは 1991 年の 2 月でした。今日 Python の作者として知られる Guido van Rossum は、alt.sources という Usenet 上のソースコード共有用のニュースグループに最初のバージョンである Python 0.9.0 を投稿しました。

Usenet は World Wide Web が生まれる以前からある情報発信ネットワークです。メール配信と似た仕組みで記事が交換され、ニュースグループというカテゴリで記事の購読やそれに関する議論ができました。

余談ですが、Ruby も最初のバージョンはネットニュース上で公開されたそうです (参考)。今では情報発信は World Wide Web を使うのが当たり前になり、ソースコードの公開は GitHub がデファクトになりましたが、当時は WWW が生まれて間もなく、情報発信はネットニュースを使うのが一般的だったようです。

Python の最初のバージョンのソースコードを見てみる

Python のソースコードは 公式ホームページ の他、GitHub からも入手することができます。

GitHub で最初のバージョンを見てみましょう。コミッターは Guido で、コミット日時は 1990 年 8 月 9 日です。ファイルは README と Makefile の二つだけで、README にはこう書かれています。

This directory contains the source to the Python documentation.
Unfortunately it's not not very readable, complete or up-to-date yet --
in other words, I'm still working on it!

<～中略～>

--Guido (last modified 10 Sep 90)

「今作ってるからちょっと待ってね」みたいなことが書かれています。

0.9.0 が見つからないので 0.9.1 を見てみる

Usenet に最初に投稿されたのは 0.9.0 ですが、残念ながらコミットグラフを見てもどのコミットが 0.9.0 なのか分かりませんでした。

代わりに、公式のダウロードページ に 0.9.1 のソースコードが公開されていたので、それをダウンロードして中身を見てみます。0.9.1 も 0.9.0 と同じ月にリリースされたようなので 内容は大きくは変わらなさそうです。

リポジトリには言語の構文を定義している Grammar というファイルがあったので中身を抜粋して見てみます。

funcdef: 'def' NAME parameters ':' suite
parameters: '(' [fplist] ')'
fplist: fpdef (',' fpdef)*
fpdef: NAME | '(' fplist ')'

これは関数定義の構文のようです。def func(param1, param2): ... という形の一般的なもののみ受け付け、キーワード引数などはまだないようです。

ただしこの定義では def func(param1, (param2, param3)): ... というような関数定義もできるようです。これは呼び出し時に func(1, (2, 3)) とすると param2 に 2 が、param3 に 3 が入って関数が実行されるようです。

print_stmt: 'print' (test ',')* [test] NEWLINE

Python 3 からは print は関数になりましたが、この時点ではまだ「文」のようです。

del_stmt: 'del' exprlist NEWLINE
pass_stmt: 'pass' NEWLINE
flow_stmt: break_stmt | return_stmt | raise_stmt
break_stmt: 'break' NEWLINE
return_stmt: 'return' [testlist] NEWLINE
raise_stmt: 'raise' expr [',' expr] NEWLINE
import_stmt: 'import' NAME (',' NAME)* NEWLINE | 'from' NAME 'import' ('*' | NAME (',' NAME)*) NEWLINE

del, pass, break, return, raise, from ... import 等のおなじみの文が定義されています。

compound_stmt: if_stmt | while_stmt | for_stmt | try_stmt | funcdef | classdef
if_stmt: 'if' test ':' suite ('elif' test ':' suite)* ['else' ':' suite]
while_stmt: 'while' test ':' suite ['else' ':' suite]
for_stmt: 'for' exprlist 'in' exprlist ':' suite ['else' ':' suite]
try_stmt: 'try' ':' suite (except_clause ':' suite)* ['finally' ':' suite]
except_clause: 'except' [expr [',' expr]]
suite: simple_stmt | NEWLINE INDENT NEWLINE* (stmt NEWLINE*)+ DEDENT

if, while, for, try-except が定義されています。

while や for には break しなかった時に実行される else 節を付けられるようですが、この時点では try 節で例外が発生しなかった時に実行される else 節は用意されていないようです。

classdef: 'class' NAME parameters ['=' baselist] ':' suite
baselist: atom arguments (',' atom arguments)*
arguments: '(' [testlist] ')'

クラス定義です。継承もサポートしているようですが、今日の Python の継承の構文とは違い、class C() = BaseClass(): ... といったように継承するようです。

Python 0.9.1 を動かしてみる

それでは、このソースコードをコンパイルしてみます。

クリーンな環境から始めたいので Docker を使うことにします。

まずは Ubuntu の最新のイメージでコンテナを起動します。

docker run -it ubuntu:latest bash

続いてコンテナの中でソースをダウンロードして展開します。

apt update -y
apt install wget -y
wget https://www.python.org/ftp/python/src/Python-0.9.1.tar.gz
tar xzvf Python-0.9.1.tar.gz
cd python-0.9.1/src/

ソースがダウンロードできたら、コンパイルに必要なパッケージをインストールして、make を実行します。

apt install build-essential -y
make

いっぱい Warning が出ましたが、カレントディレクトリに python という実行ファイルができました。実行してみます。

./python
>>> 

起動した！

関数を定義して実行してみましょう。

>>> def fib(n):
...     if n <= 1:
...         return 1
...     else:
...         return fib(n - 1) + fib(n - 2)
...
>>> for i in range(10):
...     print fib(i)
...
1
1
2
3
5
8
13
21
34
55

再帰関数もちゃんと動いているようです。

おわりに

今から約 30 年前の 1991 年に公開された Python 0.9.1 をコンパイルして動かしてみました。

30 年前というと私も生まれて間もないころで、実は前半で触れた Usenet やネットニュースも大学時代に先生方が話していたのを聞きかじった程度です。

1990 年代は WWW が生まれ急速に普及し、今日我々が使っている技術もこの時代に生まれたものが多く個人的に非常に興味がある時代です。

今回は簡単ではありますが、Python が生まれた時代のソースコードを 30 年後にタイムトラベルさせて、動いてみてもらいました。

Ceph で使われている CRUSH アルゴリズムの論文を読んだのでメモ

この記事は Ceph でオブジェクトの配置先を決定するのに使われている CRUSH アルゴリズムの論文を読んで内容を自分向けにまとめたものです。

CRUSH: Controlled, Scalable, Decentralized Placement of Replicated Data

翻訳ではないので私の解釈が入ったり削ったりした部分があるのでご注意ください。

Introduction

CRUSH はオブジェクトの識別子を、それが保存されているデバイスにマッピングするアルゴリズムである。

ここでオブジェクトはオブジェクトグループであったり、デバイスはデバイスのリスト (オブジェクトがレプリケーションされている場合) だったりする。

従来のようなファイルごと、ディレクトリごとにマッピングを持つような手法とは違い、CRUSH はストレージクラスターの階層を表現した地図と、その中でのオブジェクトの配置ルールだけを使ってマッピングを行うのでコンパクトである。

このアプローチは 2 つの点で有効である:

1. クライアントはそれぞれ独立に、オブジェクトの配置位置を導出できる (つまり Read/Write でボトルネックが生じにくい)
2. デバイスが追加されたり削除されたりした時しかメタデータ (地図のこと) が変化しない (つまりほぼ静的である)

Related Work

CRUSH は従来研究と比べて以下の点が進歩している:

• オブジェクト配置の偏りを減らすための再配置や、デバイスの重み付けが考慮されている
• オブジェクトの配置場所を決定するのに、コンパクトなクラスター地図と決定性のマッピング関数だけを使う。これは特にデータの書き込みの時に効果的で、特定の中央サーバーを介さずに、クライアントが独自にオブジェクトの配置場所を導出できる (別に読み込みの時も同様に効果的な気が？)
• 基となった RUSH アルゴリズムで課題だった信頼性とレプリケーションを改善し、パフォーマンスと柔軟性が向上している

The CRUSH algorithm

オブジェクトが配置されているデバイスは cluster map, placement rules, x (オブジェクトの識別子) だけから計算可能である。

cluster map は device と bucket で構成され、bucket を内部ノード、device を葉ノードとする木構造である。device はプロパティとして weight を持ち、bucket の weight は子ノードの weight の総和である。

この木構造はストレージクラスターの物理的な構成を反映させることを意図している。例えば HDD の一つ一つを device とし、それらを収めるサーバーをの親 bucket とし、さらにそれらのサーバーを収めるラック、それらが並ぶデータセンターのフロアの列、そしてフロア全体、といった具合に bucket でまとめていく。物理的、ネットワーク的に近いディスク同士は同時に故障する確率が高い (電源故障やネットワーク障害によって) ので、オブジェクトのレプリカを木構造的に遠くに配置することで耐障害性を高められる。

placement rules は cluster map の木構造をルートからリーフまでどのように辿るかを記述するルールのリストである。辿った先のリーフ (リーフは必ず device) がオブジェクトの配置先となるデバイスである。

placement rules は次の 3 つの関数で記述される。

x = 'オブジェクトの識別子'
trees = []  # 現在処理中の cluster map のサブツリー
devices = []  # オブジェクトの配置先となる device の一覧 (レプリカの数だけ device が選ばれる)


def take(cluster_map, trees=trees):
    """探索のルートとなるツリーをセットする
    """
    trees.clear()
    trees.append(cluster_map)


def select(num_replicas, node_label, trees=trees, x=x):
    """ツリーを辿り、node_label を持つノードを num_replicas 個選択する

       num_replicas: 選択するノードの個数
       node_label: 選択するノードのラベル (row, rack, cabinet, device 等)
    """
    subtrees = []
    for bucket in trees:
        for i in range(num_replicas):
            while True:
                # 論文ではここでデバイス故障時の対応もしていたが省略

                # 後述する決定性のアルゴリズムに従って子ノードを選択する
                child = bucket.select_child(i, x)

                if child.label != node_label:
                    bucket = child
                    continue
                else:
                    subtrees.append(child)
                    break
    trees.clear()
    trees.extend(subtrees)


def emit(trees=trees, devices=devices):
    """リーフの一覧を配置先としてセットする
    """
    devices.extend(trees)

この 3 つの関数を使い、placement rules を記述する例を示す。

今、例えば cluster map が次のようであるとする。ただし bucket(label, id), device(label, id) という書式である。

• bucket(ROOT, 'root')
  • bucket(ROW, 'row1')
    • 省略
  • bucket(ROW, 'row2')
    • bucket(CABINET, 'cabinet1')
      • device(DISK, 'disk1-1')
      • device(DISK, 'disk1-2')
      • device(DISK, 'disk1-3')
    • bucket(CABINET, 'cabinet2')
      • device(DISK, 'disk2-1')
      • device(DISK, 'disk2-2')
      • device(DISK, 'disk2-3')
    • bucket(CABINET, 'cabinet3')
      • device(DISK, 'disk3-1')
      • device(DISK, 'disk3-2')
      • device(DISK, 'disk3-3')
    • bucket(CABINET, 'cabinet4')
      • device(DISK, 'disk4-1')
      • device(DISK, 'disk4-2')
      • device(DISK, 'disk4-3')
  • bucket(row, 'row3')
    • 省略

この時、placement rules が次のようなものであるとき、

take(ROOT)
select(1, ROW)
select(3, CABINET)
select(1, DISK)
emit()

オブジェクトが配置されるデバイスは次のように決定される。

1. take(ROOT): ROOT を探索のスタート地点とする
2. select(1, ROW): ROOT 直下の ROW から一つを選ぶ。ここでは row2 が選ばれたとする
3. select(3, CABINET): row2 の子から CABINET を 3 つ選ぶ。ここでは cabinet1, cabinet3, cabinet4 が選ばれたとする
4. それぞれの cabinet の子から DISK を一つずつ選ぶ。ここでは disk1-1, disk3-2, disk4-3 が選ばれたとする
5. disk1-1, disk3-2, disk4-3 をオブジェクトの配置先とする。ここではレプリカ数は 3 となる

この他、論文ではディスクの追加／削除でレプリカの再配置がどれくらいの量起こるかが簡単に触れられていたが、ここでは割愛する。基本的には cluster map 内の総 weight のうち、追加／削除された device の weight 分、少なくとも再配置が必要になる。

また bucket には 4 つのタイプが定義されており、uniform bucket, list bucket, tree bucket, straw bucket がある。タイプごとに bucket.select_child(i, x) の計算量と、配下のデバイスの追加／削除時のレプリカの再配置効率が異なる。

	Uniform	List	Tree	Straw
計算量	O(1)	O(n)	O(log n)	O(n)
ディスク追加時の再配置の効率	悪い	非常に良い	良い	非常に良い
ディスク削除時の再配置の効率	悪い	悪い	良い	非常に良い

各 bucket のデータ構造と bucket.select_child(i, x) の計算方法が簡単に説明されていたが、これはより詳細な Ceph の実装のドキュメントを見た方がよいと判断したためここでは省略。

Evaluation

図表だけ斜め読みした。

• ディスクの追加／削除に伴うレプリカの再配置効率を、CRUSH, RUSH_p, RUSH_t について比較していた。CRUSH は追加、削除で安定して高効率な結果だった。
• uniform, list, tree, straw の 4 種の bucket について、子ノードの追加後のレプリカ再配置の効率を比較していた。straw が安定して好成績だった。
• cluster map の階層の深さの増加に伴う、計算量の増加を list, tree, straw, そして RUSH_t, RUSH_p について比較していた。RUSH_t と tree が好成績だった。
• bucket の子ノードの数の増加に伴う、計算量の増加を uniform, list, tree, straw について比較していた。理論通り、uniform は O(1)、tree は O(log n)、list, straw は O(n) なカーブを描いていた。

Future Work

• Ceph で使われている今の placement rule で十分に柔軟ではあるが、もっと柔軟に書けるシステムも存在はする
• なんらかの統計モデルを使って MTTDL (Mean Time To Data Loss) を評価する
• マッピングにはハッシュ関数が使われていて、この性能はオブジェクトへのアクセススピードやレプリカの均等な分散にも影響するので、よりよいハッシュ関数がないか調査する

おわりに

おそらく紙面の都合で、論文だけでは詳細がつかめない部分があったので他のドキュメントも続けて読んでいきたい。

• CRUSH Maps — Ceph Documentation には特にマッピングのより詳細が説明されているので読む
• Apache Hadoop 3.3.0 – HDFS Architecture は同じ分散オブジェクトストレージとして Ceph とアーキテクチャの比較をしながら読む

Win10 の WSL2 に Ubuntu をインストールして Docker 上の minikube で Flask アプリを Hello World

Kubernetes を勉強しようと思って手元の Windows に minikube の環境を構築したら、その過程でいろいろなエラーに遭遇したので解決方法を添えて手順をまとめた。

構築した環境は手元のノート PC (Windows 10 Home 64bit) に WSL2 をインストールし、それで Ubuntu を動かして、その上の Docker で minikube を動かすというもの。試しに簡単な Flask アプリをデプロイしてみた。

WSL2 の有効化と Ubuntu のインストール

Windows 上で Ubuntu を動かすために、WSL2 を有効にする。

手順は Microsoft 公式のドキュメント に従えばできた。

ただし最後、Windows Store から Ubuntu 20.04 をインストールしていざ起動してみたところ、ターミナルが立ち上がってエラーコード 0xc03a001a のエラーが発生した。これは WSL2 にしたいのにエラーが出る問題 - Qiita に従い、フォルダーのプロパティから圧縮設定を解除したら回避できた (後で気づいたが、上に挙げた Microsoft のドキュメントにもエラーコードこそなかったが対処方法は書いてあった)。

これで Windows10 の WSL2 で Ubuntu が起動できるようになった。

Ubuntu に Docker をインストール

続いて Ubuntu に Docker をインストールする。

これも Docker 公式のドキュメント に従ってインストールした。

ただし動作確認のために適当な Dockerfile をビルドしようとしたところ、cannot find cgroup mount destination: unknown というエラーが出た。このエラーは WSL2 時の Dockerコンテナの起動について – すらりん日記 に従って次のコマンドを打って回避した。

sudo mkdir /sys/fs/cgroup/systemd
sudo mount -t cgroup -o none,name=systemd cgroup /sys/fs/cgroup/systemd

これで WSL2 上の Ubuntu で Docker が動くようになった。

Ubuntu に minikube をインストール

これも基本は Kubernetes の公式ドキュメント に従ってインストールする。

今回は Docker で minikube を動かすので CPU の仮想化支援機構は必須ではない。ので grep -E --color 'vmx|svm' /proc/cpuinfo の結果が空でも OK. 手順にある「ハイパーバイザーのインストール」も必要なし。

今回は 直接ダウンロードによるMinikubeのインストール の手順を実行した。

そして minikube の起動。Docker コンテナとして minikube を動かすので

minikube start --driver=docker

で起動する。

動作確認として minikube status を打ってみる。

$ minikube status
minikube
type: Control Plane
host: Running
kubelet: Running
apiserver: Running
kubeconfig: Configured

ここまでで WSL2 上の Ubuntu で Docker コンテナとして minikube を動かせた。

Flask アプリを用意

minikube で簡単な Flask アプリを動かしてみる。Flask の公式ドキュメント にある次のサンプルコードを使う。ファイル名は app.py とする。

from flask import Flask, escape, request

app = Flask(__name__)

@app.route('/')
def hello():
    name = request.args.get("name", "World")
    return f'Hello, {escape(name)}!'

またこのアプリを動かすコンテナをビルドするための Dockerfile を用意する。

FROM python:3

RUN pip install flask

COPY ./app.py /app.py

ENV FLASK_ENV=/app.py

CMD ["flask", "run", "--host", "0.0.0.0"]

これらのファイルを

~/flast-test/
  +- app.py
  +- Dockerfile

というように配置する。

Flask アプリをビルド

このコンテナイメージをビルドしたいが、単に docker build しても後の手順がうまくいかない。いくつかポイントがあるので一つずつ説明していく。

Docker ホストの向き先の切り替え

まず、minikube は組み込みの Docker エンジンを持っていて、Kubernetes の各種デーモンやデプロイされるコンテナはこの minikube 組み込みの Docker エンジンが利用される。この組み込みの Docker エンジンは先に Ubuntu 自体にインストールした Docker とは別のものである。

この後の手順ではコンテナレジストリを使わずに、ローカルに保存されているコンテナイメージを使いたいので、minikube 組み込みの Docker エンジンの方にデプロイしたいコンテナイメージを登録する。

そのために docker コマンドで参照する Docker ホストを minikube のものに変更したい。それは次のコマンドで行う。

eval $(minikube -p minikube docker-env)

このコマンドを実行すると環境変数 DOCKER_HOST や他の必要な変数がセットされ、docker コマンドの向き先が minikube のものになる。

minikube の DNS サーバーの変更

そして docker build を行おうとすると、以下のようなエラーが出る。IP アドレスは変わり得る。

Get https://registry-1.docker.io/v2/: dial tcp: lookup registry-1.docker.io on 192.168.49.1:53: read udp 192.168.49.2:37dd860911922e: Download complete

これは minikube 内の DNS サーバーの設定がまずいので、minikube コンテナに入って /etc/resolv.conf を書き換える。それには kubernetes - Error response from daemon: Get https://registry-1.docker.io/v2/: dial tcp: lookup registry-1.docker.io...i/o timeout - Stack Overflow を参考に次の手順で行う。

minikube ssh

# 以下は minikube コンテナ内での作業
sed -E 's/nameserver .*/nameserver 8.8.8.8/' /etc/resolv.conf > resolv.conf
sudo cp resolv.conf /etc/resolv.conf
exit

これでコンテナのビルドができるようになる。

ビルド

Flask アプリを動かすコンテナをビルドしてイメージを minikube 内の Docker エンジンに登録する。

docker build ~/flask-test -t flask-test

Flask アプリを minikube にデプロイ

ようやくビルドしたコンテナを Kubernetes にデプロイできる。

まずは次のような Deployment を定義する yaml ファイルを用意する。これを ~/flask-test/deployment.yaml として保存する。

apiVersion: apps/v1
kind: Deployment
metadata:
  name: flask-test
  labels:
    app: flask
spec:
  replicas: 3
  selector:
    matchLabels:
      app: flask
  template:
    metadata:
      labels:
        app: flask
    spec:
      containers:
        - name: app
          image: flask-test:latest
          imagePullPolicy: Never
          ports:
            - containerPort: 5000

コンテナイメージは先ほどビルドしたものを使いたいので imagePullPolicy: Never としている。こうするとリモートのレジストリから Pull せずに常にローカルのイメージを使うようになる。

またレプリカ数は 3 にしている。

これを次のようにして Kubernetes に適用する。

kubectl apply -f ~/flask-test/deployment.yaml

うまくデプロイできていれば次のような結果が得られる。

$ kubectl get deployments flask-test
NAME         READY   UP-TO-DATE   AVAILABLE   AGE
flask-test   3/3     3            3           10s

$ kubectl get pods -l app=flask
NAME                         READY   STATUS    RESTARTS   AGE
flask-test-7d5c9c88b-2thh4   1/1     Running   0          10s
flask-test-7d5c9c88b-52j79   1/1     Running   0          10s
flask-test-7d5c9c88b-j6rpl   1/1     Running   0          10s

さらにこれらのコンテナに HTTP でアクセスできるように Service を定義する。

kubectl expose deployment flask-test --type NodePort

サービスが登録されていることを確認する。

$ k get services flask-test
NAME         TYPE       CLUSTER-IP      EXTERNAL-IP   PORT(S)          AGE
flask-test   NodePort   10.103.56.173   <none>        5000:31859/TCP   10s

Flask アプリへアクセス

ここまで来ればデプロイした Flask アプリにアクセスできる。まずは URL を調べるために次のコマンドを実行する。

minikube service list

|-------------|------------|--------------|---------------------------|
|  NAMESPACE  |    NAME    | TARGET PORT  |            URL            |
|-------------|------------|--------------|---------------------------|
| default     | flask-test |         5000 | http://192.168.49.2:31859 |
| default     | kubernetes | No node port |
| kube-system | kube-dns   | No node port |
|-------------|------------|--------------|---------------------------|

http://192.168.49.2:31859 でサービスが公開されていることが分かるので次のようにして Flask アプリにアクセスできる。

curl  http://192.168.49.2:31859

Hello, World!

めでたしめでたし。

Ubuntu とか Docker いらなかったかもしれない

と、手順をまとめてみて思ったが、Ubuntu とか Docker とかいらなかったかもしれない。

手元の Windows 環境を汚したくなかったので独立した Linux 環境上で Kubernetes を試したかったのだが、Docker コンテナとして minikube が動くなら Docker Desktop for Windows でもよかったかも。それか Ubuntu で直接 minikube を動かすか。

これは次回ということで。

まとめ

• WSL2 と Docker を駆使して minikube で Flask アプリを動かした
• いろいろエラー出たがエラーメッセージでググったら全部解決した
• もうちょっとシンプルな構成ができたかもしれない

参考

• Windows Subsystem for Linux (WSL) を Windows 10 にインストールする | Microsoft Docs
• WSL2 にしたいのにエラーが出る問題 - Qiita
• Ubuntu — Docker-docs-ja 1.13.RC ドキュメント
• WSL2 時の Dockerコンテナの起動について – すらりん日記
• Minikubeのインストール | Kubernetes
• Flask | The Pallets Projects
• kubernetes - Error response from daemon: Get https://registry-1.docker.io/v2/: dial tcp: lookup registry-1.docker.io...i/o timeout - Stack Overflow

ニューラルネットワークの実装

はじめに

shop.ohmsha.co.jp

わかりやすいパターン認識の第 3 章でニューラルネットワークの誤差逆伝播法が説明されていたので実装してみた。

コード

コードはこんな感じ。scikit-learn の make_moons 関数で生成したデータを学習させてみた。

from matplotlib import pyplot as plt
import numpy as np
from sklearn import datasets, model_selection


def plot_decision_boundary(data, predict):
    """ref: http://scikit-learn.org/stable/auto_examples/svm/plot_iris.html"""

    x_min, x_max = data[:, 0].min() - .5, data[:, 0].max() + .5
    y_min, y_max = data[:, 1].min() - .5, data[:, 1].max() + .5
    h = .02
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    Z = predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


class NeuralNetwork:
    EPOCH = 3000

    def __init__(self, layers, rho=1e-1):
        self.W_list = [np.random.randn(layers[i], layers[i-1] + 1)
                       for i in range(1, len(layers))]
        self.rho = rho

    def train(self, data, label):
        for i in range(self.__class__.EPOCH):
            # shuffle
            perm = np.random.permutation(len(data))
            data, label = data[perm], label[perm]

            for x, y in zip(list(data), list(label)):
                g_list = self._predict(x)

                # back propagation
                new_W_list = [np.zeros(W.shape) for W in self.W_list]
                for i in reversed(range(len(self.W_list))):
                    _g = g_list[i + 1]
                    g = g_list[i]
                    W = self.W_list[i]

                    if i == len(self.W_list) - 1:
                        # output layer
                        e = (_g - y) * _g * (1 - _g)
                    else:
                        # hidden layer
                        _W = self.W_list[i + 1][:, :-1]
                        e = np.dot(_W.T, e) * _g * (1 - _g)

                    G = np.repeat(np.concatenate([g, [1]])[np.newaxis, :],
                                  W.shape[0],
                                  axis=0)
                    E = np.repeat(e[:, np.newaxis],
                                  W.shape[1],
                                  axis=1)
                    new_W_list[i] = W - self.rho * E * G

                self.W_list = new_W_list

    def _predict(self, x):
        g_list = [x]
        for W in self.W_list:
            x = np.concatenate([g_list[-1], [1]])
            g_list.append(sigmoid(np.dot(W, x)))

        return g_list

    def predict(self, x):
        return np.argmax(self._predict(x)[-1])

    def predict_array(self, X):
        return np.array([self.predict(x) for x in list(X)])


if __name__ == '__main__':
    # prepare dataset
    moons = datasets.make_moons(n_samples=500, noise=0.1)

    x_train, x_test, y_train, y_test = model_selection.train_test_split(
        moons[0], np.eye(2)[moons[1]], test_size=0.5, shuffle=True
    )

    # train
    nn = NeuralNetwork([2, 3, 2])
    nn.train(x_train, y_train)

    # test
    errors = [y[nn.predict(x)] != 1
              for x, y in zip(list(x_test), list(y_test))]
    error_rate = len(x_test[errors]) / len(x_test)
    print(f"error rate={error_rate}")

    # display
    plot_decision_boundary(x_test, lambda x: nn.predict_array(x))

    X_c0 = x_test[np.argmax(y_test, axis=1) == 0]
    X_c1 = x_test[np.argmax(y_test, axis=1) == 1]
    plt.scatter(X_c0[:, 0], X_c0[:, 1])
    plt.scatter(X_c1[:, 0], X_c1[:, 1])

    plt.show()

結果

実行結果は以下。ちゃんと学習できてそうな雰囲気。

またエポックごとの識別エラー率をグラフにしてみたのが以下。だいたい 500 エポックくらいでエラー率が 0 に達した。

まとめ

• 誤差逆伝播法を実装した
• scikit-learn の make_moons 関数で生成したデータで学習させてみた
• 500 エポックくらいで学習できた

参考

• わかりやすい パターン認識 | 理工学専門書,情報科学,知識科学・人工知能 | Ohmsha
• sklearn.datasets.make_moons — scikit-learn 0.19.1 documentation

Widrow-Hoff の学習規則でクラス分類

はじめに

shop.ohmsha.co.jp

わかりやすいパターン認識の第 3 章で Widrow-Hoff の学習規則が説明されていたので実装してみた。

コード

コードはこんな感じ。それぞれ 2 次元正規分布に従う 2 クラスのパターンで学習してみた。パターンはわざとクラス間で一部重なるようにしておいて、線形分離できないケースを試してみた。

from matplotlib import pyplot as plt
import numpy as np


class WidrowHoff:
    EPOCH = 100

    def __init__(self, n_dim, n_class, rho=1e-3):
        self.W = np.random.randn(n_class, n_dim + 1)
        self.rho = rho

    def train(self, data, label):
        for i in range(self.__class__.EPOCH):
            # shuffle
            perm = np.random.permutation(len(data))
            data, label = data[perm], label[perm]

            for x, y in zip(list(data), list(label)):
                # update weight
                X = np.repeat(np.array(list(x) + [1])[np.newaxis, :],
                              self.W.shape[0],
                              axis=0)
                E = np.repeat((self._predict(x) - y)[:, np.newaxis],
                              self.W.shape[1],
                              axis=1)
                self.W = self.W - self.rho * E * X

    def _predict(self, x):
        x = np.array(list(x) + [1])
        return np.dot(self.W, x)

    def predict(self, x):
        return np.argmax(self._predict(x), axis=0)


if __name__ == '__main__':
    # prepare dataset
    X_c0 = 5 * np.random.randn(100, 2)
    X_c1 = 5 * np.random.randn(100, 2) + np.array([10, 10])

    data = np.concatenate([X_c0, X_c1])
    label = np.array([[1, 0] for i in range(100)] +
                     [[0, 1] for i in range(100)])

    # train
    widrow_hoff = WidrowHoff(n_dim=2, n_class=2)
    widrow_hoff.train(data, label)

    # show
    plt.scatter(X_c0[:, 0], X_c0[:, 1])
    plt.scatter(X_c1[:, 0], X_c1[:, 1])

    w = widrow_hoff.W[0] - widrow_hoff.W[1]
    y = lambda x: w[0] / -w[1] * x + w[2] / -w[1]
    x = np.arange(-10, 20, 0.1)
    plt.plot(x, y(x))

    plt.show()

結果

こんな感じで決定境界が引けた。なんとなくそれっぽい境界になってそう。

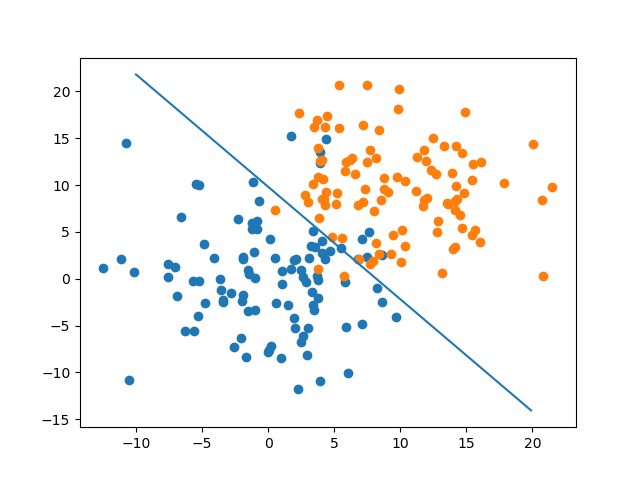
そしてエポックごとにその時点での識別精度をグラフにしたものが以下。

今回のデータはそれぞれ平均が (0, 0) と (10, 10)、標準僅差が 5、x と y は独立の 2 次元正規分布を使ったことを考えると、(0, 0) と (10, 10) 間の距離 / 2 / 5 = 1.4142... ということで、標準正規分布で 1.414 よりも上側の確率と識別精度は一致するはず。

正規分布表を参照するとだいたい 0.079 くらいなので、グラフの値とおおよそ一致した。

まとめ

• Widrow-Hoff でクラス分類してみた
• 線形分離不可能なパターンでもいい感じに境界引けた
• 識別性能も理論値とだいたい一致した

参考

• わかりやすい パターン認識 | 理工学専門書,情報科学,知識科学・人工知能 | Ohmsha
• 統計学入門 - 東京大学出版会